La duplicación del cubo
Vamos a comenzar este capítulo recordando, y ampliando, algunos conceptos que ya vimos en el capítulo 2. Lo haremos a través de la solución del siguiente problema.
Problema: Cortar, en una cantidad finita de partes, una franja de longitud infinita de modo tal que las partes resultantes permitan armar la misma franja y además un cuadrado. (Por una franja de longitud infinita entendemos la región del plano comprendida entre dos rectas paralelas, incluidas las dos rectas).
Para resolver el problema, fijamos un cuadrado cualquiera dentro la franja. A la derecha de este cuadrado fijamos un segundo cuadrado. A la derecha de este último, a la misma distancia, fijamos un tercer cuadrado. Y así sucesivamente. De este modo, habremos fijado una sucesión infinita de cuadrados, cada uno equidistante con sus dos vecinos (excepto el primero, por supuesto, que no tiene vecino a la izquierda).
Dividimos la franja de la siguiente manera:1. Una parte está formada por el primer cuadrado.
2. Otra parte está formada por todos los demás cuadrados de la sucesión.
3. Una tercera parte está formada por todos los demás puntos de la franja.
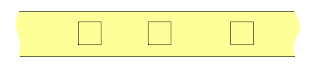
La figura siguinete nos muestra cómo reorganizar estas partes de modo de obtener la franja más un cuadrado.
El primer cuadrado es desplazado fuera de la franja. Todos los demás son desplazados una misma distancia hacia la izquierda. De este modo, obtenemos la misma franja más un cuadrado-
Como vimos en el segundo capítulo, un conjunto de puntos forma una "parte" si a todos los puntos en cuestión se les aplica simultáneamnete los mismos movimientos (rotaciones, traslaciones, simetrías). Por lo tanto, es válido considerar a todos los cuadrados (excepto el primero) conjuntamente como una sola parte.
Como he dicho unos párrafos más arriba, esta idea ya la vimos en el capítulo 2. Me interesa destacar aquí que el hecho de que la cantidad de partes sea finita o infinita depende, en algunos casos, de nuestro ingenio a la hora de definir esas partes. Por ejemplo, en el caso de la franja, si los cuadrados hubieran sido elegidos a distancias crecientes (así como en el problema del cap. 2, los "segmentos rojos" estaban colocados a distancias decrecientes) entonces cada cuadrado habría sido una parte diferente y la cantidad total de partes habría sido infinita.
Hay casos, sin embargo, en los que, no importa cuánto ingenio depleguemos, la cantidad de partes no puede ser finita, veremos algún ejemplo más adelante.Con esta idea en mente, revisemos otra vez al problema del capítulo anterior:
Problema: Cortar un cuadrado en partes de modo de obtener dos cuadrados iguales al original.
En el capítulo anterior, para dividir el cuadrado elegimos un lado cualquiera de él y lo cortamos en segmentos perpendiculares a ese lado. Ahora bien ¿cada segmento constituye una parte diferente? En realidad, según la idea que acabamos de ver, no tenemos suficiente información como para responder esa pregunta. Necesitamos saber exactamente qué movimientos se les aplica a los segmentos.
Por ejemplo, si hubiera todo un grupo de segmentos a los que se les aplicaran simultáneamente los mismos movimientos, entonces en conjunto, esos segmentos formarían una sola parte. En principio al menos, es concebible que, inclusive, la cantidad total de partes pudiera llegar a ser finita (tal como en el ejemplo de la franja).
Para saber si, en el problema del cuadrado, la cantidad de partes es finita, o no, debemos volver a resolver el problema, pero ahora indicando de manera explícita los movimientos involucrados.
Recordemos que la solución se basó en el hecho de que hay tantos puntos en un segmento como en dos segmentos de la misma longitud que él. Esto significa que es posible emparejar los puntos de un segmento con los puntos de dos segmentos de la misma longitud. Mostrmos explícitamente cómo se puede hacer este emparejamiento. Lo haremos en cuatro pasos sucesivos.
Paso 1: Hay tantos puntos en un segmento como en en un segmento del doble de longitud que él.
Queremos ver cómo es posible emparejar cada punto de un segmento A con un punto de un segmento B (del doble de longitud que A) de modo que ningún punto quede sin pareja, ni que haya dos o más puntos que queden emparejados con un mismo punto (ni solteros, ni polígamos, como decíamos en el capítulo anterior). El siguiente dibujo muestra cómo emparejar los puntos de un segmento con otro del doble de longitud:
De paso, este dibujo resuelve el siguiente problema: cortar un segmento en partes que, reordenadas, nos den un segmento del doble de longitud. Cada parte, en este caso, es un punto y las líneas azules nos dicen cómo debemos desplazarlos (cada punto sufre un desplazamiento diferente, por lo que debe ser considerado una parte diferente).
Paso 2: Hay tantos puntos en un segmento como en un segmento de la misma longitud al que le hemos quitado uno de los extremos. (La falta del extremo se indica con un "circulito blanco". Como ya dijimos en otras ocasiones, se trata solamente de una convención gráfica para indicar una situación matemática irreproducible en la realidad física.)
Es obvio que hay un emparejamiento uno-a-uno entre dos segmentos de la misma longitud: cada punto de un segmento lo emparejamos con el punto correspondiente del otro. ¿Pero qué pasa si a uno de los segmentos le falta uno de los extremos? El dibujo siguiente nos muestra qué podemos hacer en ese caso (en el fondo, es la misma idea que la empleada más arriba para la franja infinita o, en el cap. 2 para los "segmentos rojos").
Tomamos uno de los extremos del segmento que está "completo" y lo emparejamos con el punto medio del otro segmento. Al punto medio del primer segmento lo emparejamos con el punto que marca un cuarto de la longitud. Al que marca un cuarto de la longitud con el de un octavo, y así sucesivamente. Todos los demás puntos se asocian con su pareja "natural" (la que le correspondería si no hubiera faltado ningún punto).
Paso 3: Veamos este dibujo.
En la figura, tomamos un segmento y lo partimos en dos. Una de las partes contiene el punto medio del segmento original, la otra no lo contiene. La parte que no contiene el punto medio es emparejada con una de la misma longitud que sí tiene los mismos extremos.
Paso 4: A cada uno de los dos segmentos obtenimos en el paso anterior le aplicamos el procedimiento indicado en el paso 1. La combinación de todos estos emparejamientos (la "composición" de los movimientos, se diría en leguaje matemático) nos da como resultado una manera de emparejar los puntos de un segmento con los de dos segmentos de la misma longitud que él.
Para duplicar el cuadrado, tal como ya dijimos en el capítulo anterior, aplicamos estos cuatro pasos a uno de los lados de la figura y hacemos que cada punto "arrastre" al segmento contenido en el cuadrado y que es perpendicular al lado elegido.
De este modo, una vez más, hemos logrado la duplicación del cuadrado. Una observación cuidadosa de los movimientos empleados nos permite concluir (ahora sí) que la cantidad de partes usadas es infinita, ya que, en efecto, cada segmento es una parte diferente (dado que a cada segmento se le aplica una traslación diferente).
Ahora bien, los cuatro pasos que vimos antes nos permiten duplicar el segmento. La duplicación del cuadrado puede verse como la "consecuencia plana" de esa duplicación lineal. Podemos ir un paso más allá y usar la duplicación del cuadrado para duplicar el cubo.
En efecto, pensemos al cuadrado superior del dibujo anterior como la base de un cubo. Cada segmento de los que antes usamos para duplicar ese cuadrado nos servirá ahora como "guía" para hacer un corte perpendicular en el cubo. El cubo queda así cortado en lonjas cuadradas unidimensionales. Si hacemos que cada segmento arrastre la lonja correspondiente, las lonjas formarán dos cubos iguales al original.
Es decir, hemos resuelto el siguiente problema: cortar un cubo en partes que permitan armar dos cubos iguales al original.
La duplicación del cubo se basa, en definitiva, en el hecho de que hay una correspondiencia uno-a-uno entre los puntos de un segmento y los putnos de dos segmentos de la misma longitud que él. Pero este hecho ya era conocido por Georg Cantor hacia 1875. Es decir, Cantor, aunque (que yo sepa) nunca lo publicó, ya sabía que era posible duplicar un cubo. El Teorema de Banach-Tarski se publicó en 1926, casi 50 años después ¿cuál es, entonces, el mérito de Banach y Tarski?
La posibilidad de duplicar un volumen era ya conocida en 1875, el mérito de Banach y Tarski (1) es haber tenido la habilidad suficiente como lograr esa duplicación en una cantidad finita de partes. Volveremos a esta cuestión en el próximo capítulo.
Nota: (1) Aclaremos que Alfred Tarski y Stephan Banach fueron dos grandes matemáticos que estarían, por mérito propio, en la historia de esa ciencia, aun cuando nunca hubieran duplicado la esfera.
(Continuara...)
