La vida de Alicia -
La liberación de la cooperante se debe en buena medida a la decisión de un iluminado: Abú Hannas
JOSÉ MARÍA IRUJO - Madrid - 10/03/2010
La liberación de la cooperante española Alicia Gámez, secuestrada por uno de los batallones de Al Qaeda en el Magreb Islámico (AQMI), se debe en buena medida a la decisión de un iluminado: Abderramán, Abú Hannas, el denominado juez del desierto, un dirigente religioso del que sólo existe una fotografía, la que aparece en los vídeos, oculto bajo su turbante mientras lanza soflamas incendiarias sobre la necesidad de crear un nuevo califato y un Gobierno islámico en el Magreb. Sus discursos terminan siempre con la coletilla: "Pido a Alá morir por la yihad".
"Mi felicidad sólo será completa cuando regresen Albert y Roque"
Aún quedan dos rehenes españoles por liberar
Abu Hannas, de unos 30 años, ha tenido un papel trascendental en la decisión de liberar a Alicia Gómez, según señalan a EL PAÍS fuentes próximas a la negociación. El grupo que retiene a los cooperantes españoles consultó a Hannas que hacer con la española y éste recomendó su liberación por el hecho de ser una mujer.
Un manual clandestino sobre secuestros redactado supuestamente por Hannas y encontrado en 2008 en un piso del popular barrio Takrkzaina, de Nuakchot, la capital de Mauritania, titulado La ley de los prisioneros extranjeros, explica qué hacer y cómo tratar a los secuestrados. El documento establece que si hay una mujer entre los secuestrados se la puede tomar como esposa o liberarla, finalmente Hannas ha impuesto la puesta en libertad de Alicia Gómez por el hecho de ser mujer, según señalan fuentes cercanas a la negociación.
El manual, intervenido a uno de los salafistas más sanguinarios de AQMI, señala que si los secuestrados son enemigos (militares, policías o agentes secretos) hay autorización para matarlos; si no lo son, se debe negociar un rescate económico o un intercambio de prisioneros. Este es el caso de los otros dos secuestrados españoles Roque Pascual y Albert Vilalta por los que se pide, además de dinero, la puesta en libertad de varios presos de AQMI recluidos en el fortín de Lahsar en Nuakchot.
El manual, un puñado de folios escritos en árabe, se encontró en la casa donde se refugió Jahen Olsaman, un islamista sospechoso de participar en el asesinato de cuatro franceses, una familia con dos menores que disfrutaba sus vacaciones de Navidad a 250 kilómetros de la capital mauritana. Olsalam purga hoy su pena en la cárcel de Lahsar junto con otros 60 miembros de AQMI, y, según algunas fuentes, es uno de los presos cuya liberación exigen los secuestradores para soltar a los españoles.
El dirigente religioso Abu Hannas, jugaba en el Bohdid, un equipo de fútbol local de un barrio en Nuakchot, tenía novia y trabajo, pero su obsesión por los estudios coránicos le condujeron por el camino vidrioso y oscuro que lleva a la yihad. Era imán en una pequeña mezquita y su verbo fácil le convirtió en un referente para un ejército de fieles que escuchaba ensimismado sus discursos cada vez más extremistas. Nadie sabe quién lo captó para la nueva base de Al Qaeda en África, pero desde hace varios años se ha convertido en la voz religiosa del grupo salafista que atenta y secuestra en el desierto del Sahel.
El joven mauritano es el "aliento espiritual" de un grupo terrorista que necesitaba un referente religioso propio y cercano y es quien marca los límites de lo que se debe o no hacer, según aseguran fuentes próximas a los salafistas. La fuerte expansión de AQMI ha obligado a sus dirigentes a tener un juez del desierto que explique sus acciones y decisiones y las bendiga para sentirse respaldados. Por ese motivo se cree que la posición de Abú Hannas será determinante en el futuro de los secuestrados españoles. "Están en sus manos porque él tendrá que autorizar y explicar la decisión que se adopte", aseguran varias fuentes consultadas.
Las condiciones para formar parte de este ejército de terroristas escondido en los desiertos fueron redactadas por Abú Hannas, según la policía mauritana. Se les pide tener conocimientos técnicos o informáticos, estar dispuestos a convertirse en suicidas y un documento de idoneidad firmado por el jefe de reclutadores de la región.
AQMI, según fuentes de la inteligencia francesa y mauritana, cuenta hoy con cuatro brigadas diferentes repartidas por el inmenso desierto del Sahel, una extensa región que va desde el océano Atlántico hasta el mar Rojo, un territorio de nadie donde Gobiernos débiles y fallidos no tienen medios para combatir el terrorismo. Agrupan a unos 300 hombres, en su mayoría argelinos, y sus nombres son: Tarek Ibn Ziyad, que en febrero de 2008 secuestró a varios turistas austriacos en Túnez; la Brigada de los turbantes, compuesta por algunos tuaregs, aliados de AQMI en Malí; Ansar, cuyo símbolo explica sin rodeos que su misión es secuestrar a cristianos; y Farkan. El dirigente religioso de todos ellos es este ex futbolista y recitador del Corán.
Abú Hannas tuvo problemas para ser aceptado por algunos argelinos y en sus primeros discursos llegó a confesar que se sentía más cerca de éstos que de sus paisanos mauritanos. Las dificultades terminaron cuando Abú Musad Abde I Wadud, el emir del Grupo Salafista para la Predicación y el Combate (GSPC) argelino, le dio su bendición, le nombró juez del desierto y miembro del Consejo de AQMI. Wadud fue quien anunció en 2006 la alianza de los salafistas argelinos con Osama Bin Laden y es el auténtico impulsor de la expansión de AQMI, un grupo que ha logrado agrupar a yihadistas de, al menos, siete nacionalidades bajo la misma bandera.
El dirigente religioso mauritano no ha sido nunca detenido, su vida y andanzas por el desierto están llenas de leyendas que corren de boca en boca por las mezquitas más radicales de Mauritania. "Es muy inteligente y sabe cómo llegar a la gente. Sus discursos son muy agresivos y buscan despertar las conciencias y captar nuevos militantes", señala un joven próximo a los presos mauritanos de Al Qaeda. El pasado mes de junio, Abú Hannas lanzó un llamamiento a los mauritanos para que no acudieran a las urnas. "Todo es mentira. La democracia es una farsa. No vayáis a votar", reclamó.
¿Cómo se ha extendido el salafismo en Mauritania?, se preguntan muchos en este país de 3,3 millones de habitantes donde hace años era imposible ver a una mujer con burka. Muchas miradas se dirigen a las ruinas de la universidad Mohamed Ibn Saud, financiada por el Gobierno de Arabia Saudí, cerrada en 2003 y derribada hasta convertirse hoy en una escombrera en el centro de la ciudad. "Ahí empezó a cocerse todo", asegura Ahmed, un joven profesional mauritano. En 2004, el Gobierno secuestró los 2.000 ejemplares del periódico Al Khabar. El diario informaba de que Ayman Al Zawahiri, el escudero egipcio de Bin Laden, hacía un llamamiento a Mauritania para que se uniera a la yihad. "Nos llamaron mentirosos y manipuladores. Intentaron ocultar lo que ya estaba ocurriendo", explica Mohamed Lamil, hoy residente en España.
Escuchar los discursos claros y contundentes de Abú Hannas produce escalofríos. En su última grabación, con el preludio de una música de fondo que anima a la lucha, el juez del desierto mauritano, el tipo que puede decidir sobre el futuro de Alicia Gómez, Roque Pascual y Albert Vilalta, decía frases como éstas: "No hay un Gobierno islámico de verdad. Todos son teatros y cristianos... Estamos aquí para construir el mundo islámico de nuevo... Nuestra alianza es una pesadilla para nuestros enemigos. Vamos a ganar esta guerra contra el ejército de Satán". Y terminaba con su remate final: "Pido a Alá morir por la yihad".
Información actualizada del reportaje publicado el 20/12/2009 'El juez del desierto'
La Paradoja de Banach-Tarski (Cap. 6)
La duplicación del cubo
Vamos a comenzar este capítulo recordando, y ampliando, algunos conceptos que ya vimos en el capítulo 2. Lo haremos a través de la solución del siguiente problema.
Problema: Cortar, en una cantidad finita de partes, una franja de longitud infinita de modo tal que las partes resultantes permitan armar la misma franja y además un cuadrado. (Por una franja de longitud infinita entendemos la región del plano comprendida entre dos rectas paralelas, incluidas las dos rectas).
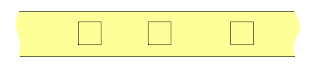
Para resolver el problema, fijamos un cuadrado cualquiera dentro la franja. A la derecha de este cuadrado fijamos un segundo cuadrado. A la derecha de este último, a la misma distancia, fijamos un tercer cuadrado. Y así sucesivamente. De este modo, habremos fijado una sucesión infinita de cuadrados, cada uno equidistante con sus dos vecinos (excepto el primero, por supuesto, que no tiene vecino a la izquierda).
 Dividimos la franja de la siguiente manera:
Dividimos la franja de la siguiente manera:1. Una parte está formada por el primer cuadrado.
2. Otra parte está formada por todos los demás cuadrados de la sucesión.
3. Una tercera parte está formada por todos los demás puntos de la franja.
La figura siguinete nos muestra cómo reorganizar estas partes de modo de obtener la franja más un cuadrado.

El primer cuadrado es desplazado fuera de la franja. Todos los demás son desplazados una misma distancia hacia la izquierda. De este modo, obtenemos la misma franja más un cuadrado-
Como vimos en el segundo capítulo, un conjunto de puntos forma una "parte" si a todos los puntos en cuestión se les aplica simultáneamnete los mismos movimientos (rotaciones, traslaciones, simetrías). Por lo tanto, es válido considerar a todos los cuadrados (excepto el primero) conjuntamente como una sola parte.
Como he dicho unos párrafos más arriba, esta idea ya la vimos en el capítulo 2. Me interesa destacar aquí que el hecho de que la cantidad de partes sea finita o infinita depende, en algunos casos, de nuestro ingenio a la hora de definir esas partes. Por ejemplo, en el caso de la franja, si los cuadrados hubieran sido elegidos a distancias crecientes (así como en el problema del cap. 2, los "segmentos rojos" estaban colocados a distancias decrecientes) entonces cada cuadrado habría sido una parte diferente y la cantidad total de partes habría sido infinita.
 Hay casos, sin embargo, en los que, no importa cuánto ingenio depleguemos, la cantidad de partes no puede ser finita, veremos algún ejemplo más adelante.
Hay casos, sin embargo, en los que, no importa cuánto ingenio depleguemos, la cantidad de partes no puede ser finita, veremos algún ejemplo más adelante.Con esta idea en mente, revisemos otra vez al problema del capítulo anterior:
Problema: Cortar un cuadrado en partes de modo de obtener dos cuadrados iguales al original.
En el capítulo anterior, para dividir el cuadrado elegimos un lado cualquiera de él y lo cortamos en segmentos perpendiculares a ese lado. Ahora bien ¿cada segmento constituye una parte diferente? En realidad, según la idea que acabamos de ver, no tenemos suficiente información como para responder esa pregunta. Necesitamos saber exactamente qué movimientos se les aplica a los segmentos.
Por ejemplo, si hubiera todo un grupo de segmentos a los que se les aplicaran simultáneamente los mismos movimientos, entonces en conjunto, esos segmentos formarían una sola parte. En principio al menos, es concebible que, inclusive, la cantidad total de partes pudiera llegar a ser finita (tal como en el ejemplo de la franja).
Para saber si, en el problema del cuadrado, la cantidad de partes es finita, o no, debemos volver a resolver el problema, pero ahora indicando de manera explícita los movimientos involucrados.
Recordemos que la solución se basó en el hecho de que hay tantos puntos en un segmento como en dos segmentos de la misma longitud que él. Esto significa que es posible emparejar los puntos de un segmento con los puntos de dos segmentos de la misma longitud. Mostrmos explícitamente cómo se puede hacer este emparejamiento. Lo haremos en cuatro pasos sucesivos.
Paso 1: Hay tantos puntos en un segmento como en en un segmento del doble de longitud que él.
Queremos ver cómo es posible emparejar cada punto de un segmento A con un punto de un segmento B (del doble de longitud que A) de modo que ningún punto quede sin pareja, ni que haya dos o más puntos que queden emparejados con un mismo punto (ni solteros, ni polígamos, como decíamos en el capítulo anterior). El siguiente dibujo muestra cómo emparejar los puntos de un segmento con otro del doble de longitud:

De paso, este dibujo resuelve el siguiente problema: cortar un segmento en partes que, reordenadas, nos den un segmento del doble de longitud. Cada parte, en este caso, es un punto y las líneas azules nos dicen cómo debemos desplazarlos (cada punto sufre un desplazamiento diferente, por lo que debe ser considerado una parte diferente).
Paso 2: Hay tantos puntos en un segmento como en un segmento de la misma longitud al que le hemos quitado uno de los extremos. (La falta del extremo se indica con un "circulito blanco". Como ya dijimos en otras ocasiones, se trata solamente de una convención gráfica para indicar una situación matemática irreproducible en la realidad física.)
Es obvio que hay un emparejamiento uno-a-uno entre dos segmentos de la misma longitud: cada punto de un segmento lo emparejamos con el punto correspondiente del otro. ¿Pero qué pasa si a uno de los segmentos le falta uno de los extremos? El dibujo siguiente nos muestra qué podemos hacer en ese caso (en el fondo, es la misma idea que la empleada más arriba para la franja infinita o, en el cap. 2 para los "segmentos rojos").
Tomamos uno de los extremos del segmento que está "completo" y lo emparejamos con el punto medio del otro segmento. Al punto medio del primer segmento lo emparejamos con el punto que marca un cuarto de la longitud. Al que marca un cuarto de la longitud con el de un octavo, y así sucesivamente. Todos los demás puntos se asocian con su pareja "natural" (la que le correspondería si no hubiera faltado ningún punto).
Paso 3: Veamos este dibujo.

En la figura, tomamos un segmento y lo partimos en dos. Una de las partes contiene el punto medio del segmento original, la otra no lo contiene. La parte que no contiene el punto medio es emparejada con una de la misma longitud que sí tiene los mismos extremos.
Paso 4: A cada uno de los dos segmentos obtenimos en el paso anterior le aplicamos el procedimiento indicado en el paso 1. La combinación de todos estos emparejamientos (la "composición" de los movimientos, se diría en leguaje matemático) nos da como resultado una manera de emparejar los puntos de un segmento con los de dos segmentos de la misma longitud que él.
Para duplicar el cuadrado, tal como ya dijimos en el capítulo anterior, aplicamos estos cuatro pasos a uno de los lados de la figura y hacemos que cada punto "arrastre" al segmento contenido en el cuadrado y que es perpendicular al lado elegido.

De este modo, una vez más, hemos logrado la duplicación del cuadrado. Una observación cuidadosa de los movimientos empleados nos permite concluir (ahora sí) que la cantidad de partes usadas es infinita, ya que, en efecto, cada segmento es una parte diferente (dado que a cada segmento se le aplica una traslación diferente).
Ahora bien, los cuatro pasos que vimos antes nos permiten duplicar el segmento. La duplicación del cuadrado puede verse como la "consecuencia plana" de esa duplicación lineal. Podemos ir un paso más allá y usar la duplicación del cuadrado para duplicar el cubo.
En efecto, pensemos al cuadrado superior del dibujo anterior como la base de un cubo. Cada segmento de los que antes usamos para duplicar ese cuadrado nos servirá ahora como "guía" para hacer un corte perpendicular en el cubo. El cubo queda así cortado en lonjas cuadradas unidimensionales. Si hacemos que cada segmento arrastre la lonja correspondiente, las lonjas formarán dos cubos iguales al original.
Es decir, hemos resuelto el siguiente problema: cortar un cubo en partes que permitan armar dos cubos iguales al original.
La duplicación del cubo se basa, en definitiva, en el hecho de que hay una correspondiencia uno-a-uno entre los puntos de un segmento y los putnos de dos segmentos de la misma longitud que él. Pero este hecho ya era conocido por Georg Cantor hacia 1875. Es decir, Cantor, aunque (que yo sepa) nunca lo publicó, ya sabía que era posible duplicar un cubo. El Teorema de Banach-Tarski se publicó en 1926, casi 50 años después ¿cuál es, entonces, el mérito de Banach y Tarski?
La posibilidad de duplicar un volumen era ya conocida en 1875, el mérito de Banach y Tarski (1) es haber tenido la habilidad suficiente como lograr esa duplicación en una cantidad finita de partes. Volveremos a esta cuestión en el próximo capítulo.
Nota: (1) Aclaremos que Alfred Tarski y Stephan Banach fueron dos grandes matemáticos que estarían, por mérito propio, en la historia de esa ciencia, aun cuando nunca hubieran duplicado la esfera.
(Continuara...)
"salvad al pringao WILLY"

10-Se plantea el arrebato del ordago mayor...SE PUEDE COSER UNA BOCA PARA QUE LUEGO lo que salga del culo no APESTE A PUTREFACTO REFRITO chabacanero? yo, adalid de lo que se da en llamar "libertad de palabro democritter chungiforme", ni me decanto ni me decameron...solo espero que sigan las PAPANATAS A TOPE, que ya es dificil de por si levantarse todos los dias ignorando el fanatismo fantastique de este nuestro perolero post-lazarillo "his father was a SANGRIATOR"...YEE! y que cunda la felicidad
El miedo (Mario Benedetti)
No se juega con el miedo porque el miedo puede ser un arma de defensa propia, una forma inocente o culpable del coraje. El miedo nos abre los ojos y nos cierra los puños y nos mete en el riesgo desaprensivamente. Andamos por el mundo con el miedo a cuestas como si fuera un pudor obligatorio o en su defecto una variable del fracaso. Tal vez sea el mandamiento, o tal vez el mandamiento de alguna desconocida ley, de un dios cualquiera. Por las dudas, una buena fórmula contra el miedo puede ser la que dejó escrita el bueno de Pessoa: "espera lo mejor y prepárate para lo peor".
Del libro Vivir adrede
Publicado por Pedro Javier en el blog azuldelmar jueves, febrero 25, 2010.
Otro problema de probabilidades
Abel, Bruno, Carlos, Diego, Esteban y Federico (para abreviar, A, B, C, D, E y F) llegan tarde a la clase de Matemáticas. El Prof. Zacarías (Z, para los amigos) les pregunta el motivo del retraso y ellos contestan que se debe a que el automóvil en el que viajaban (los seis juntos) ha sufrido una pinchadura en una rueda y que han perdido tiempo cambiando la goma (o , si se quiere, el neumático) correspondiente.
El Prof. Z duda de la veracidad del relato y, a modo de comprobación, les pide inmediatamente que se sienten en pupitres separados y que cada uno anote en un papel cuál fue la rueda averiada (puede ser la delantera derecha, la delantera izquierda, la trasera derecha o la trasera izquierda). El razonamiento de Z es que si los seis no indican exactamente la misma rueda, entonces podrá afirmar que los alumnos están mintiendo.
Hasta aquí el relato plagia prolijamente un problemita publicado por Martin Gardner en uno de sus libros. Démosle ahora una pequeña vuelta de tuerca. Supongamos que, en efecto, los alumnos hayan mentido, que no hubo ninguna rueda averiada y que llegaron tarde por cualquier otro motivo (inconfesable).
Demos por supuesto, además, que los alumnos elegirán al azar qué rueda van a escribir. Zacarías se pregunta...
1. ¿Cuál es la probabilidad de que los seis anoten la misma rueda?
Gastón, que es otro alumno, ha visto que A y B lograron intercambiar, sin que Z lo notara, unas señas. Gracias a ellas, se han puesto de acuerddo en anotar ambos una rueda delantera, pero no llegaron acordar si anotarán la derecha o la izquierda (cada uno elegirá al azar una de ambas). En base a esta información, Gastón se pregunta...
2. ¿Cuál es la probabilidad de que los seis anoten la misma rueda?
Horacio ha visto lo mismo que Gastón, y ha visto además que C y D también lograron ponerse de acuerdo en escribir ambos una rueda delantera, aunque no pudieron acordar si la derecha o la izquierda. En base a esta información, Horacio se pregunta...
3. ¿Cuál es la probabilidad de que los seis anoten la misma rueda?
Inés, finalmente, ha visto lo mismo que Gastón y Horacio, pero además ha visto que E y F se han puesto de acuerdo... aunque no entendió bien si se pusieron de acuerdo en escribir ambos una rueda delantera o ambos una rueda trasera. Sí es seguro que, como en los dos casos anteriores, no lograron acordar si sería la rueda derecha o la izquierda. En base a esta información, Inés se pregunta...
4. ¿Cuál es la probabilidad de que los seis anoten la misma rueda?
Finalmente...
5. ¿Cuál es la probabilidad "real" de que los seis anoten la misma rueda?